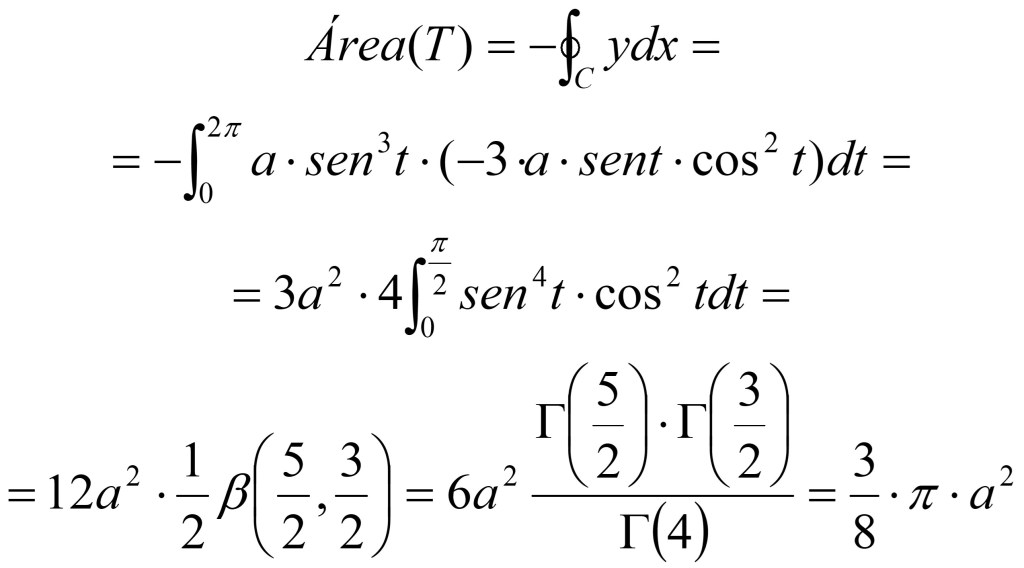“Geometría es arte; el área, su medida.”

“Calcular un área es traducir la geometría en memoria: un número que guarda el espacio vivido dentro de sus límites.” -Carlos ipiens-

Algo de historia y un primer enunciado:

1. Antecedentes

El teorema se enmarca en el cálculo vectorial y en la relación entre integrales de línea y de superficie (o de área, en el plano).

• Desde el siglo XVII, con Newton y Leibniz, se conocía que la integral de una derivada en un intervalo se relaciona con los valores en los extremos (Teorema Fundamental del Cálculo).
• En el siglo XVIII, matemáticos como Euler, Clairaut, Lagrange y Gauss empezaron a buscar generalizaciones de este principio en dimensiones mayores.

---

2. George Green (1793–1841)

El Teorema de Green fue formulado por primera vez por el autodidacta inglés George Green en 1828 en su famoso Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism.

• Green no era matemático académico, sino molinero, y publicó su ensayo costeándolo por suscripción local.
• En ese trabajo introdujo lo que hoy conocemos como funciones de Green y varias identidades integrales, incluyendo la que después se llamaría Teorema de Green.
• El teorema relaciona una integral de línea alrededor de una curva cerrada con una integral doble en la región encerrada.

---

3. Riemann (1826–1866) y la conexión con el análisis complejo

Bernhard Riemann, unas décadas después, usó el teorema como herramienta fundamental en la teoría de funciones de variable compleja.

• El Teorema de Green aplicado a las funciones holomorfas se convierte en la fórmula integral de Cauchy, pieza central del análisis complejo.
• En algunos textos antiguos de matemáticas se encuentra el nombre “Teorema de Green–Riemann” para destacar este puente entre el análisis real y el complejo.

---

4. Desarrollo posterior

• A mediados y finales del siglo XIX, el teorema fue reconocido como un caso particular de un resultado mucho más general: el Teorema de Stokes (siglo XIX, atribuido a Sir George Stokes).
• El Teorema de Green es la versión bidimensional del de Stokes.
• Hoy se estudia en cursos de cálculo multivariable y análisis complejo.

5. enunciado y demostración

Teorema de Green-Riemann

Sean P(x,y) y Q(x,y) dos Campos Escalares derivables y con derivadas continuas en un recinto S del plano XY, y su curva frontera C de Jordan y regular. Sea T la unión de C y su interior S. Bajo estas condiciones se satisface la siguiente igualdad:

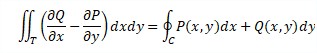
Demostración:

Para probar esta igualdad, bastará probar  las dos igualdades siguientes:

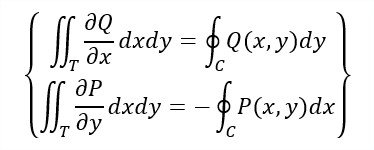
Veamos  primero que:

a) Comenzamos por obtener :

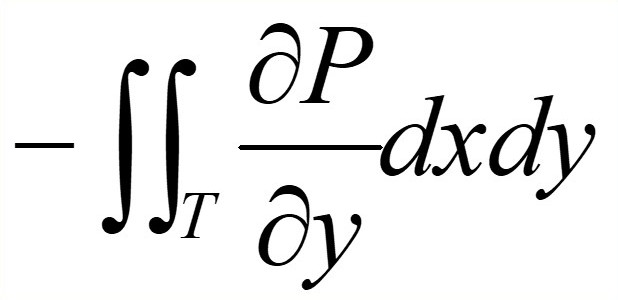
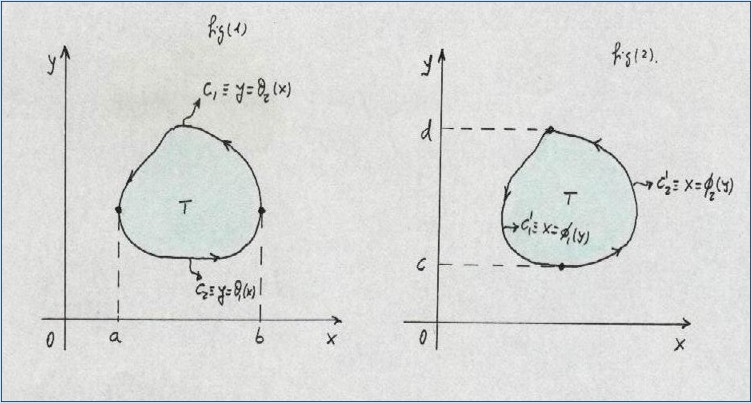
Para ello consideremos la figura (1)

Se tiene:

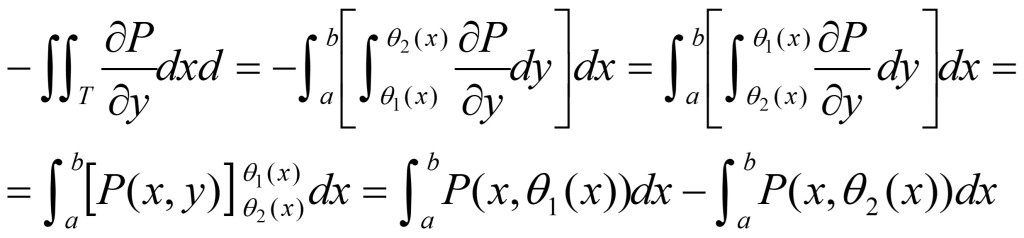
b) Veamos el valor del segundo miembro:

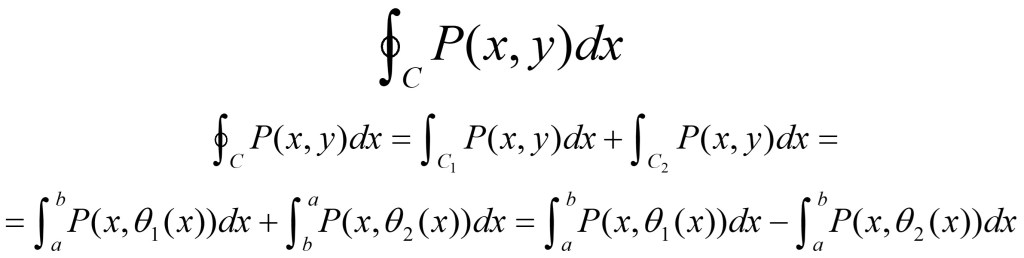
•Comparando los resultados obtenidos en los apartados a) y b) anteriores, queda probada la igualdad:

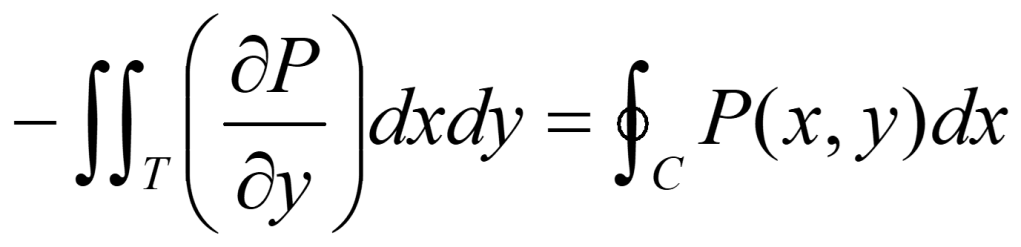
•Del mismo modo, con solo considerar la figura (2), puede probarse que:

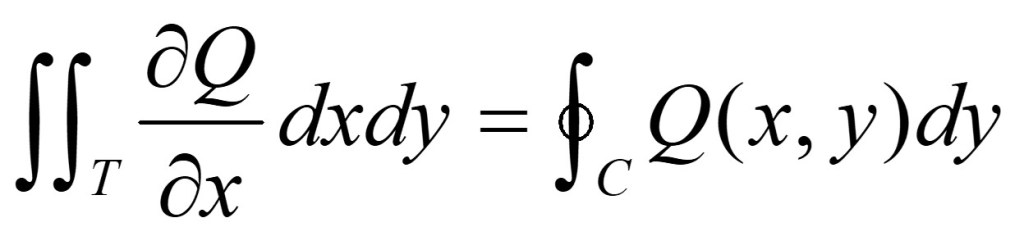
•Y considerando los resultados anteriores, se tiene probada la igualdad que asegura el Teorema:

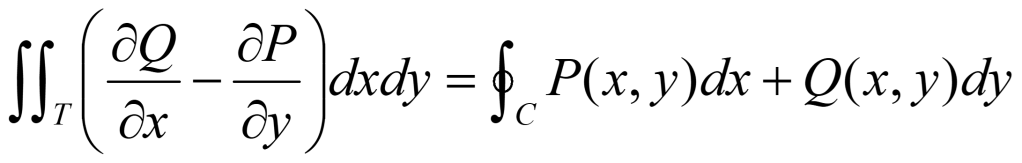
Nota importante

Nota: Para recintos más generales en los que no se cumpla que ninguna paralela a los ejes corte a C en más de dos puntos, el recinto se podrá dividir en sub-recintos cuyas fronteras si cumplan las condiciones o hipótesis del teorema. Véase figura:

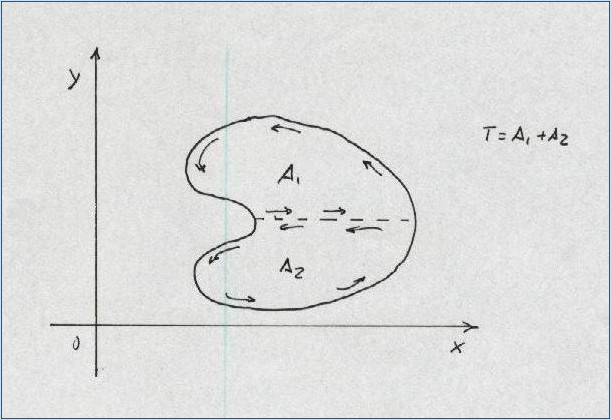
6. Aplicaciones

6.1. Cálculo de una Integral Curvilínea mediante una Integral Doble.

6.2. Cálculo de una Integral Doble mediante una Integral de Línea.

6.3. Cálculo del área de un recinto plano. Como ejemplo de esta aplicación obtendremos el Área del Astroide como veremos en el siguiente apartado. Veamos esta aplicación más detenidamente.

•Una forma cómoda para la obtención del Área, sería definiendo las funciones escalares P(x,y)  y  Q(x,y) del siguiente modo:

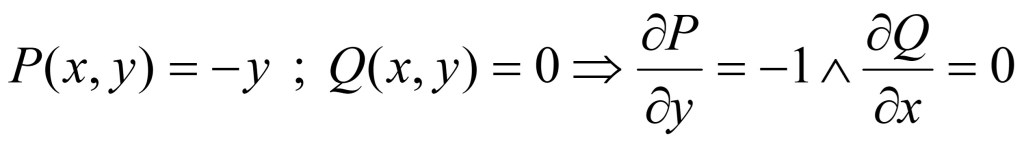
•Así, se tiene:

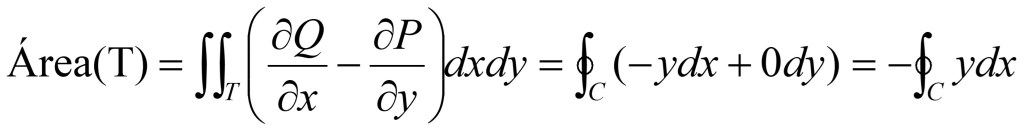
O también haciendo:

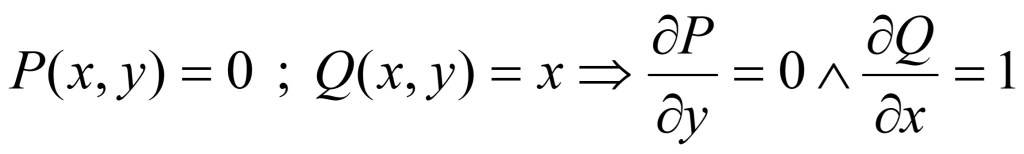
Obtenemos:

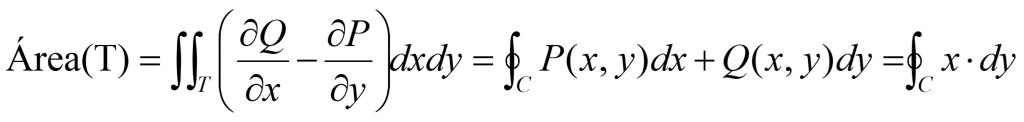
6.4. Obtención de un Volumen mediante una integral de línea.

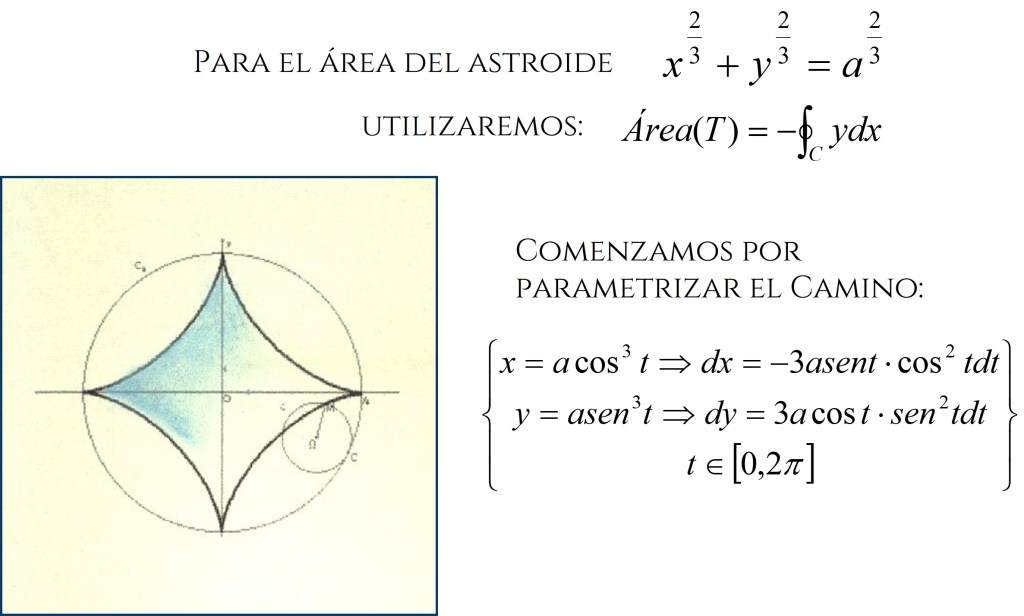
área del astroide

Definición

En matemática, un astroide es un tipo particular de hipocicloide , una curva con cuatro vértices . Los astroides son también curvas de Lamé : todos los astroides son versiones a escala de la curva especificada por la ecuación:

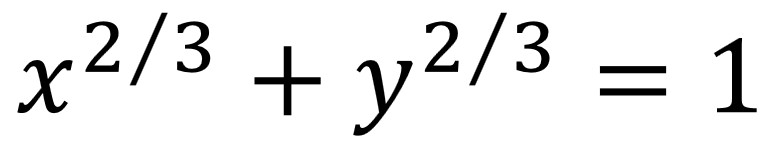
El camino que sigue un punto de una 
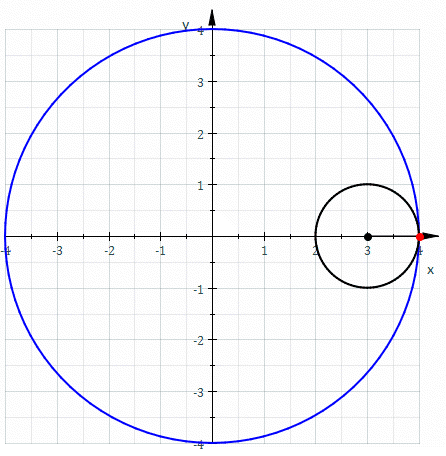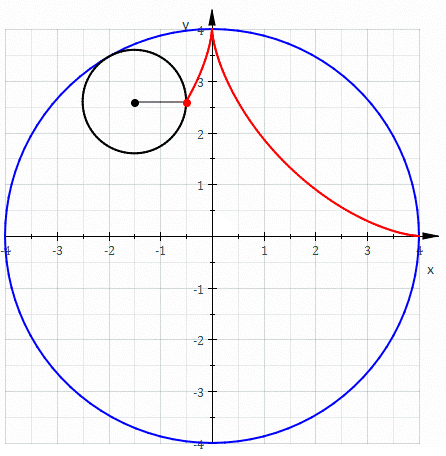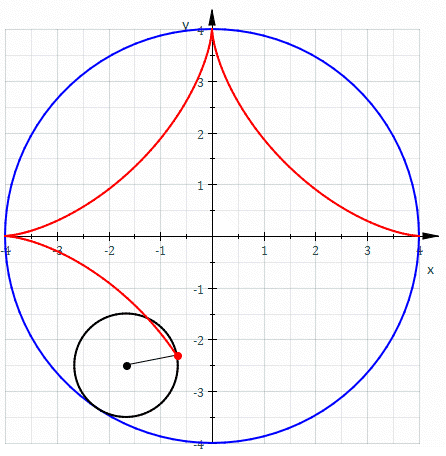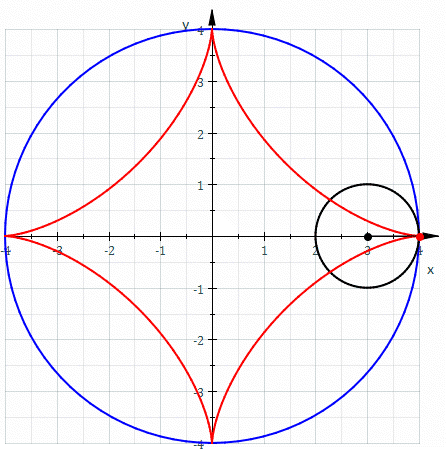
circunferencia de radio 1/4 rodando dentro de una circunferencia del radio 1 traza un astroide.

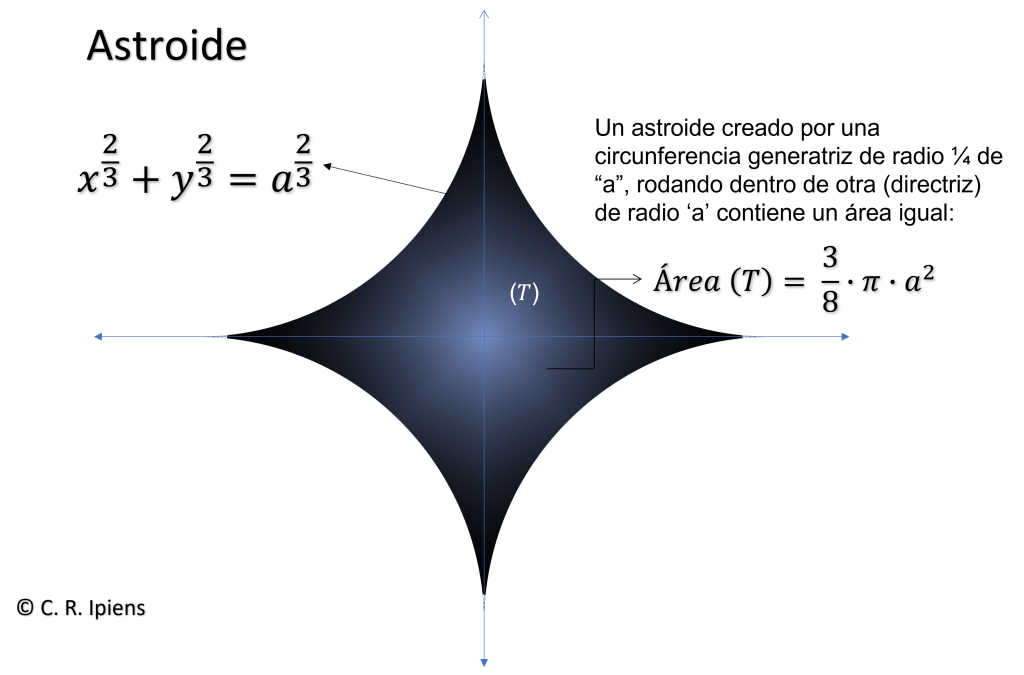
Para el cálculo del Área del Astroide, haremos uso del apartado 6.3. de las aplicaciones del teorema vistas anteriormente. Y en el proceso de cálculo haremos uso herramientas conocidas como la parametrización de un camino y las funciones Gamma y Beta.

El área será: